动态规划-初试
动态规划
「动态规划 dynamic programming」它将一个问题分解为一系列更小的子问题,并通过存储子问题的解来避免重复计算,从而大幅提升时间效率。
动态规划只能应用于有最优子结构的问题。「最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决。」
解题思路
每个人对同一件事都有不同的理解,这里的思路也只提供借鉴
判断题目是否可以用动态规划解决
大问题可以拆分为小问题
是否有最优子结构:小问题的解能解决大问题的解
求大问题的解如何拆分为小问题的解
推导出最优子结构
推导状态转移方程(递推公式)
验证公式
求解【解题方式:迭代 > 记忆化搜索 > 递归】
确定边界
确定状态转移方向
求解之道 - 基础
爬楼梯(简单)
问题
问题:爬楼梯,力扣:https://leetcode.cn/problems/climbing-stairs/submissions/480628139/
给定一个共有 n 阶的楼梯,每步可以上 1 阶或者 2 阶,请问有多少种方案可以爬到楼顶。
分析
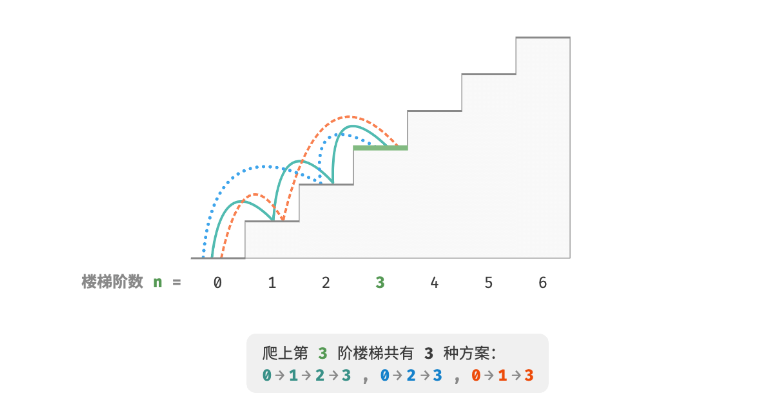
探索分析题目:我们先手动求解一下题目,设F(n)为第n阶楼梯的方案。
f(1) = 1;
f(2) = 2;
f(3) = 3;
f(4) = 5;
f(5) = 8;
......
通过列举几个示例,我们会发现,如果要走到第n个台阶,那么只有两种情况,要么从n-1阶台阶走1阶上去,要么从n-2阶走2阶上去。
得出规律:
f(n) = f(n - 1) + f(n - 2);
f(n - 1) = f(n - 2) + f(n - 3);
f(n - 2) = f(n - 3) + f(n - 4);
......
简单罗列后,要想求出f(n),就必须求出 n-1 阶台阶和 n-2 阶台阶的方案,要求出 n-1 阶台阶的方案,就必须求出求出 n-2 阶台阶和 n-3 阶台阶的方案......递推得知最终需要求 1 阶台阶和 2 阶台阶的方案。从得出的规律可以看出有很多结果是被重复计算的,例如: f(n - 2)、f(n - 3) 等等,我们称为子问题。既然有重复计算,我们就可以用数据结构暂存结果来避免计算子问题,符合动态规划思想,将大问题拆解成一系列子问题求解。
最优子结构是否满足探讨:
因为我们得出的规律f(n) = f(n - 1) + f(n - 2),大问题依赖小问题,小问题又依赖更小的问题,得出小问题的解最终可得大问题的解,符合最优子结构。
求解
使用map(记忆化搜索)
java中我们最常用的结构就是map,这里我们使用map暂存子问题,来求得结果。【当然,因为我们的map的key是int类型,所以也可以使用数组暂存结果】
public int solutionMap(int n) {
// 暂存子问题
Map<Integer, Integer> subMap = new HashMap<>();
subMap.put(1, 1);
subMap.put(2, 2);
for (int i = 3; i <= n; i++) {
subMap.put(i, subMap.get(i - 1) + subMap.get(i - 2));
}
return subMap.get(n);
}通过执行结果我们可以看到,效率没问题,但是因为使用了Map,所以占用了部分内存。

时间复杂度:因为只有一次for循环,循环的次数为n,所以时间复杂度为 O(n)
空间复杂度:使用了Map暂存结果大小,map的大小为n,所以空间复杂度为 O(n)
使用递归(暴力搜索)
通过我们得出的规律 f(n) = f(n - 1) + f(n - 2),我们会发现,这个公式符合深度优先搜索(dfs),所以我们可以通过递归的方式解决问题。
public int solutionRecursion(int n) {
if (n == 1 || n == 2) {
return n;
}
return solutionRecursion(n - 1) + solutionRecursion(n - 2);
}放到力扣上执行,发现超时了。

通过列出来递归树,我们可以看到很多子问题都在重复计算,我们没有暂存子问题的结果,虽然省内存了,但是确带来了时间复杂度的指数级增长。每次递归,都会产生两个计算结果,每个计算结果又会拆分成2个,递归n次,则会生成 2^n个结果,因为最后n==1或n==2的时候不再需要递归,所以这里还需要-1,当然这个-1并不会最终影响时间复杂度:O(n) = 2^n
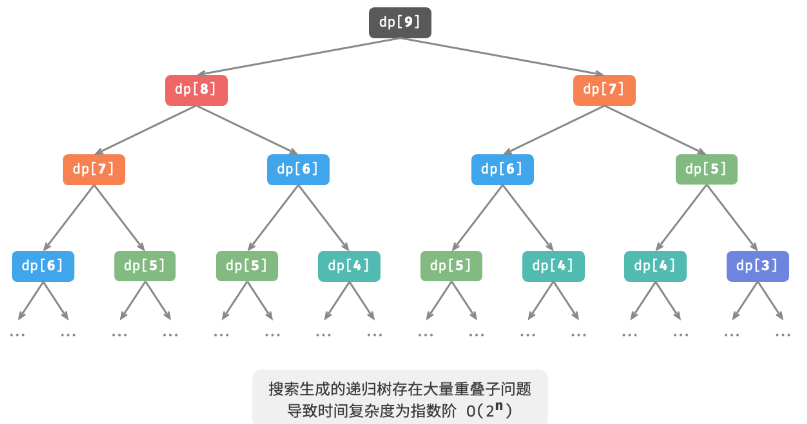
时间复杂度:因为递归的调用深度为n,每次会新生成2个结果,所以时间复杂度为 O(2^n)
空间复杂度:虽然没有使用变量暂存结果,但是递归也需要占用内存,递归的调用深度为n,所以空间复杂度为 O(n)
使用迭代(最优解-动态规划)
一般的递归的实现可以改成迭代的方式,我们将递归的方法改成迭代。
这里因为需要记录 f(n - 1) 和 f(n - 2) 的结果,所以需要至少两个变量去记录中间结果,这里我们的res1是 f(n - 2) ,res2 是 f(n - 1)。

通过上述表格我们可以看到,res1的结果是上一轮的res2,res2是上一轮res1 + res2,因为变量存在覆盖,我们需要先计算res2,在计算res1,这样我们可以得出两个表达式:
res2 = res1 + res2;
res1 = res2 - res1;
public int solutionIteration(int n) {
if (n == 1 || n == 2) {
return n;
}
int res1 = 1;
int res2 = 2;
for (int i = 3; i <= n; i++) {
res2 = res2 + res1;
res1 = res2 - res1;
}
return res2;
}力扣运行结果通过,这里的内存使用我们可以忽略,因为使用的是Java,运行的方法多多少少会需要创建其他的对象去做一些额外的事情。我们通过代码可以看到,我们将原来的map改成了2个变量,内存的使用肯定是下降的。

时间复杂度:算法只有一个for循环,最多循环n次,所以时间复杂度为 O(n)
空间复杂度:不管n的大小,算法只使用了3个变量,空间复杂度为常数级,O(1)
斐波那契数(简单)
力扣题目链接: https://leetcode.cn/problems/fibonacci-number/
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。
斐波那契数跟爬楼梯差不多,只是初始值变了,小伙伴自行尝试求解
不同路径(中等)
问题
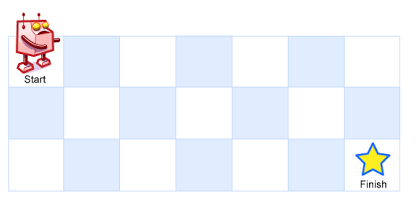
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28
分析
我们将纵坐标设为m,横坐标设为n,求到坐标点的路径数为 f(m, n)。
这题跟爬楼梯类似,因为机器人只能往下走和往右走,所以如果机器人要到达坐标点 (m, n) 只能从 (m - 1, n) 和 (m, n - 1) 这两个坐标过去,继续向下推论,那机器人要导到坐标 (m-1, n) 呢,同理,也是只能从两个坐标点过去,因为我们推论:f(m, n) = f(m - 1, n) + f(m, n - 1)。
横坐标为0的一列和纵坐标为行的一列,因为只有一个方式可以到达,所以横纵坐标的值都为1。
验证推论:
验证推论的步骤就是将几个示例带入求解,看是否满足表达式,此处省略验证。
求解
动态规划求解
这里我们使用了一个二位数组dp求解,因为二位数组符合表达式两个坐标的要求。【当然这个也能优化为使用一维数组,这里我们不做探讨】
「刚开始接触二维dp数组的时候总是犯晕迷糊,这里也希望小伙伴能坚持下去,当看到的场景多了,就不惧怕了」
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
// 循环计算
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}力扣执行通过

时间复杂度:前两次循环的次数分别为m和n,均为常数,双层循环的次数为m*n,所以时间复杂度为 O(m * n)
空间复杂度:使用一个二位的dp数组用于临时存储中间结果,数组的大小为m*n,所以空间复杂度为O(m * n)
不同路径II(中等)
问题
这是不同路径题目的变体,添加障碍物,网格中的障碍物和空位置分别用
1和0来表示。传入的是二位数组,问从左上角到右下角将会有多少条不同的路径?示例1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右
分析
这是上一题的变体,通过分析我们发现,可以继续沿用上一题的表达式 f(m, n) = f(m - 1, n) + f(m, n - 1)。
需要单独处理障碍物的问题,通过分析我们得知,当机器人碰到障碍物时,假设这个障碍物的坐标是 (m, n),此路则完全不同,即机器人到达该点的路径数为0,因为有了障碍物,我们在循环的时候额外判定障碍物即可。
需要额外注意的是,题目并没有说明障碍物一定会出现在哪个坐标,这里有两个需要额外注意的坐标,一个是起点,一个是终点,如果这两个点有障碍物的话,可想而知,机器人的路径数为0。
求解
继续沿用上一次的解,添加障碍物的判定。需要额外注意:如果是第一行或第一列上出现障碍物,那行或列后面的路径数都应该为0,所以第一行的坐标的路径数依赖他的左侧的第一个坐标,第一列同理,最终得出,我们需要初始化起点坐标的路径数作为参考。
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
// 判断起点是否可走
int[][] dp = new int[m][n];
if (obstacleGrid[0][0] == 1) {
dp[0][0] = 0;
} else {
dp[0][0] = 1;
}
// 初始化
for (int i = 1; i < m; i++) {
// 碰到障碍物,到达改点的路径数为0
if (obstacleGrid[i][0] == 1) {
dp[i][0] = 0;
} else {
dp[i][0] = dp[i - 1][0];
}
}
for (int j = 1; j < n; j++) {
// 碰到障碍物,到达改点的路径数为0
if (obstacleGrid[0][j] == 1) {
dp[0][j] = 0;
} else {
dp[0][j] = dp[0][j - 1];
}
}
// 循环计算
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
// 碰到障碍物,到达改点的路径数为0
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}力扣执行结果:

障碍物的添加不影响时间复杂度和空间复杂度,同上一题
时间复杂度:O(m * n)
空间复杂度:O(m * n)
整数拆分
问题
给定一个正整数
n,将其拆分为k个 正整数 的和(k >= 2),并使这些整数的乘积最大化。返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。示例 2:
输入: n = 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
分析
很多小伙伴拿到这个题的时候感觉思路跟动态规划扯不上关系,因为要求拆分的个数 >=2,那我们慢慢分析。
分析是否可以使用动态规划
这里我们定义 f(n) 为整数n拆分后最大的乘积,我们尝试将问题拆分,这里要求拆分的个数 >=2,这里我们先分开讨论这两种情况:
(1)当拆分整数的个数为2时,我们假定 f(i) 为数字 i 的整数拆分最大乘积,拆分的两个数字假定为 j、i - j ,那两个数值的乘积为 j * (i - j)
(2)当拆分整数的个数大于2时,我们假定 f(i) 为数字 i 的整数拆分最大乘积,拆分的整数我们可以分为两部分,j 和 另一部分,另一部分我们可以数量肯定是超过3个的,这样我们无法像拆分两个数字一样直接计算乘积,那我们直接用表达式 dp[i - j] 表示,那这两部分的乘积为 j * dp[i - j]
(3)通过分析我们可以看出大问题可以拆分成子为题解决,并且符合最优子结构
递推表达式
(1)通过上述的分析,我们可以得出最大的乘积为 max( j (i - j), j dp[i - j])
(4)因为需要拆分多次,还需要跟 dp[i] 比较, max(dp[i], max( j (i - j), j dp[i - j]))
验证递推表达式
这里我们将几组数据带入验证接口,这里不做过多讨论。
求解
通过表达式我们可以看出,循环需要从前往后求解,因为 dp[0] 和 dp[1] 均为无效解,我们这里不作考虑,dp[2] = 1。第二层循环是拆分的正整数,从1开始拆分,递增最大值不能超过 i / 2,或者不能超过 i - j 即可,避免不必要的重复(例如 10的1和9、9和1是相同的)。
public int integerBreak(int n) {
if (n < 2) {
return 0;
}
int[] dp = new int[n + 1];
dp[2] = 1;
for (int i = 3; i <= n; i++) {
for (int j = 1; j <= i / 2; j++) {
dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
}
}
return dp[n];
}力扣结果:

时间复杂度:因为有双层循环,虽然第二层循环小于n,但我们也看做近似n,那时间复杂度为O(n^2)
空间复杂度:使用了长度为 n+1 的dp数组,1为常数,所以空间复杂度为 O(n)