动态规划

「动态规划 dynamic programming」它将一个问题分解为一系列更小的子问题，并通过存储子问题的解来避免重复计算，从而大幅提升时间效率。

动态规划只能应用于有最优子结构的问题。「最优子结构的意思是局部最优解能决定全局最优解。简单地说，问题能够分解成子问题来解决。」

疑问，什么使用用max

解题思路

每个人对同一件事都有不同的理解，这里的思路也只提供借鉴

判断题目是否可以用动态规划解决
- 大问题可以拆分为小问题
- 是否有最优子结构：小问题的解能解决大问题的解
求大问题的解如何拆分为小问题的解
- 推导出最优子结构
- 推导状态转移方程（递推公式）
- 验证公式
求解【解题方式：迭代 > 记忆化搜索 > 递归】
- 确定边界
- 确定状态转移方向

求解之路-背包问题

0-1背包问题

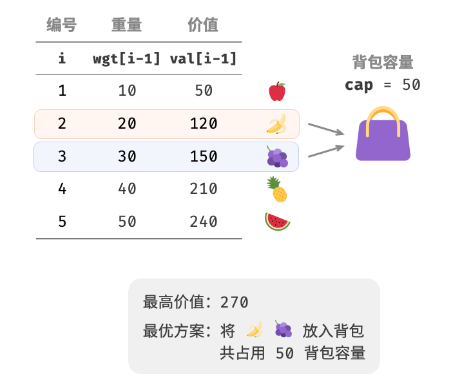
问题

给 m 个物品，第 i 个物品的重量为 wgt[i − 1]、价值为 val[i − 1] ，和一个容量为 n 的背包。每个物品只能选择一次，问在不超过背包容量下能放入物品的最大价值。

分析

对于物品i，只有放入和不放入两种情况
- 不放入物品i，背包里的物品价值不变，背包里的剩余容量不变
- 放入物品i，背包里物品的价值增加 val[i - 1]，背包的剩余容量减少 wgt[i - 1]
通过上述我们可以看到，我们最终求的是价值，影响价值的有两个因素，物品i是否放入（放入才有价值），以及背包的剩余容量n。这里我们假定 dp[i, c] 为第 i 个物品在背包剩余容量为 c 的时候背包中的最大值。这里因为dp依赖两个变量，所以dp数组的大小为
(m + 1),(n + 1) 的二位数组。
最优子结构：
- 不放入物品i，背包的最大值为 dp[i - 1, c]，因为物品不放入，剩余容量仍为c
- 放入物品i，背包的最大值为 dp[i - 1, c - wgt[i - 1]] + val[i - 1]，因为物品放入，剩余容量为c - wgt[i - 1]，这里价值取的 dp[i - 1, c - wgt[i - 1]] 为当前物品不放入的最大值，为什么取剩余容量为c - wgt[i - 1]，是因为剩余的容量需要能放入物品 i ；最大价值增加第i个物品的价值 val[i - 1]
- 综合取最大值：dp[i, c] = max(dp[i - 1, c], dp[i - 1, c - wgt[i - 1]] + val[i - 1]),
- 这里需要注意对于物品i，如果剩余的容量 c 不足以放下物品i，只能选择不放入
确定边界以及转移方向
- 当i为0，就是没有任务物品的时候，则价值为0
- 当c为0，通过表达式我们可以看到物品的最大值与前一个物品的最大值有关联，因为dp[0][0] 为 0，所以一整行都为0
- 通过表达式可以看出，第i物品的最大值依赖第 i - 1个物品的最大值，所以我们正常变量二位数组即可

求解

这里需要注意第i个物品无法放入的情况，即不放入物品，则最大值为上一个物品放入的最大值。

// m 一个有m个物品，n为背包容量，wgt为每个物品的重量，val为每个物品的价值
public int backpack01(int m, int n, int[] wgt, int[] val) {
    // dp[i, c] = max(dp[i - 1, c], dp[i - 1, c - wgt[i - 1]] + val[i - 1])
    int[][] dp = new int[m + 1][n + 1];

    // 初始化，这里不设置也行，默认0
    for (int i = 0; i < m; i++) {
        dp[i][0] = 0;
    }
    for (int j = 0; j < n; j++) {
        dp[0][j] = 0;
    }

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            // 这里需要注意第i个物品是否能放入背包
            if (wgt[i - 1] > j) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - wgt[i - 1]] + val[i - 1]);
            }
        }
    }

    return dp[m][n];
}

力扣没有相关题目，这里我们采用案例执行的方式

输出结果为：20

@Test
public void fun01() {
 int m = 3;
 int n = 4;
 int[] wgt = new int[]{1, 2, 3};
 int[] val = new int[]{5, 11, 15};

 System.out.println(backpack01(m, n, wgt, val));
}

我们使用了二位数组存储，方便理解，但是分析我们会发现，第i个物品肯定与第i - 1 个物品的价格有关联，所以可以优化为一维数组

时间复杂度：双层循环，O(m, n) = m * n

空间复杂度：dp数组，O(m, n) = (m + 1) (n + 1) =mn + m + n + 1, 取值 m n 即可

优化

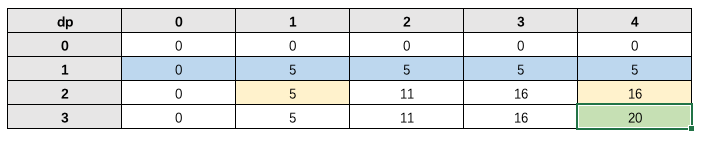
这里我花了一下上图的值变化以及依赖关系，通过图我们可以看出数值是按整行变化的，所以我们可以将二维数组改成一维数组；

当我们要计算绿色坐标的值时，需要依赖上一行的坐标1和4的值，如果我们第二层循环正常遍历，则当前行的1坐标的值会直接替掉上一行的1坐标的值，导致结果覆盖，所以我们从前往后计算，不会有覆盖的情况。

public int backpack01Optimize(int m, int n, int[] wgt, int[] val) {
    // dp[i, c] = max(dp[i - 1, c], dp[i, c - wgt[i - 1]] + val[i - 1])
    int[] dp = new int[n + 1];

    for (int i = 1; i <= m; i++) {
        // 倒序遍历
        for (int j = n; j >= 1; j--) {
            // 这里需要注意第i个物品是否能放入背包
            if (wgt[i - 1] <= j) {
                dp[j] = Math.max(dp[j], dp[j - wgt[i - 1]] + val[i - 1]);
            }
        }
    }

    return dp[n];
}

完全背包

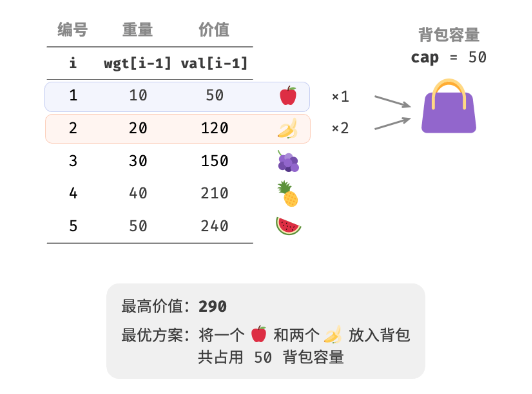
问题

给定 m 个物品，第 i 个物品的重量为 wgt[i − 1]、价值为 val[i − 1] ，和一个容量为 n 的背包。每个物品可以重复选取，问在不超过背包容量下能放入物品的最大价值。

分析

对于物品i，有放入和不放入两种选择，我们这里定义dp为 dp[i, c]
- 不放入物品：最大值为 dp[i - 1, c]，最大值与上一个物品 i - 1 的最大值相同，并且剩余容量不变
- 放入物品：最大值为 dp[i, c - wgt[i - 1]] + val[i - 1]，这里为什么是 i 而不是 i - 1 呢，因为物品i是可以被重复放入的，所以物品 i 放入的最大值应该取当前物品 i 是否放入的最大值。
最优子结构
- dp[i, c] = max(dp[i - 1, c], dp[i, c - wgt[i - 1]] + val[i - 1])
边界和转移方向
- 当i为0，就是没有任务物品的时候，则价值为0
- 当c为0，通过表达式我们可以看到物品的最大值与前一个/当前物品的最大值有关联，因为dp[0][0] 为 0，剩余容量又为0，所以一整行都为0
- 因为当前物品的最大值与前一个/当前物品的最大值有关联，所以正序遍历即可

求解

求解过程跟0-1背包差不多，只是dp公式不一样了，当然这个也可以优化为一维数组，这里不做过多赘述。

/**
 * 完全背包问题
 * dp[i, c] = max(dp[i - 1, c], dp[i, c - wgt[i - 1]] + val[i - 1])
 */
public int completeBackpack(int m, int n, int[] wgt, int[] val) {
    int[][] dp = new int[m + 1][n + 1];

    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (wgt[i - 1] > j) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - wgt[i - 1]] + val[i - 1]);
            }
        }
    }

    return dp[m][n];
}